Multidimensional item response theory modeling (mIRT) 

mIRT is a family of psychometric models useful for supporting the design and development of multidimensional assessments such as those aligned to the NGSS (Reckase, 2009). These mIRT approaches to educational measurement are useful when the aim is to align instruction and assessment (Ackerman, 1992; Walker & Beretvas, 2006). The SIPS mIRT approach assumes that the tasks, by design, are assessing more than one dimension—indeed, most will be designed to measure the three salient dimensions of disciplinary core ideas (DCIs), crosscutting concepts (CCCs), and science and engineering practices (SEPs). Using a PAD approach to task design and development, we will augment the mIRT models, which may differ across grade levels, with additional information about task features captured during the design stage. Our goal is to identify features of the assessment tasks that contribute in instructionally meaningful ways to understanding students’ science learning and, ultimately, to provide teachers with actionable diagnostic classifications of their students. By using a measurement approach that integrates descriptive analyses, classical test theory methods (Crocker & Algina, 2006), and mIRT, we expect to identify unique patterns of mastery and non-mastery of relevant knowledge and skills and use the model-based ability estimates to inform classroom level score reports and to support richly descriptive student-level reports. 

Because this integrated measurement approach is both confirmatory (e.g., confirming task difficulty parameters) and diagnostic, the design of the NGSS aligned tasks will require identifying, a priori, the measurement targets (i.e., the performance expectations) as well as the sets of KSAs underpinning student achievement. Those evidence identification processes will be specified early in the task design process by applying a PAD method described earlier (e.g., evidence-centered design, Mislevy & Haertel, 2006). Moreover, within the NGSS instructional framework, tasks are comprised of a number of subtasks (or items); thus, the assessment tasks are, by design, multidimensional. The task–KSA alignment as determined by the PAD process will be captured and instantiated in a series of psychometric “explanatory” models. The integration of the mIRT models and the task/item feature identification methods contribute to construct validity and ensure the accuracy of the inferences drawn about student learning and the instructional utility of the task specifications and feature. This measurement approach, we believe, is particularly attractive because the supplemented mIRT models present a psychometrically sound solution when multidimensional feedback is needed to improve alignment with instruction. We assume—the idea remains to be tested—that this modeling approach, informed by a science learning progressions framework, will work with a relatively constrained number of unique tasks at each grade-level and relatively small samples of students. 

Embedded Standard Setting & Embedded Methods

Embedded Standard Setting

Embedded Standard Setting (ESS; Lewis & Cook, 2020) recognizes that the alignment of test items to performance levels, either by design during item inception or as the result of an independent alignment study, may be substituted for the judgments made during traditional item-based standard settings (e.g., Bookmark, ID Matching, etc.). When subject matter experts’ (SMEs) item-PLD alignments are supported by empirical data, cut scores can be estimated that optimize the consistency of SME item-PLD alignments with empirical data. Thus, under ESS, cut scores are estimated by optimizing the evidentiary relationship between items and the claims and measurement targets articulated in the PLDs.

Embedded Standard Setting has several requirements, including (a) the development of well-articulated PLDs, (b) assessment items that are aligned to the PLDs by design or as a result of an independent alignment study, and (c) empirical data that support the item-PLD alignments. When these requirements are met, cut scores emerge organically as a direct result of the coherence of the PLDs, assessment items, item-PLD alignments, and empirical data.

Embedded Methods

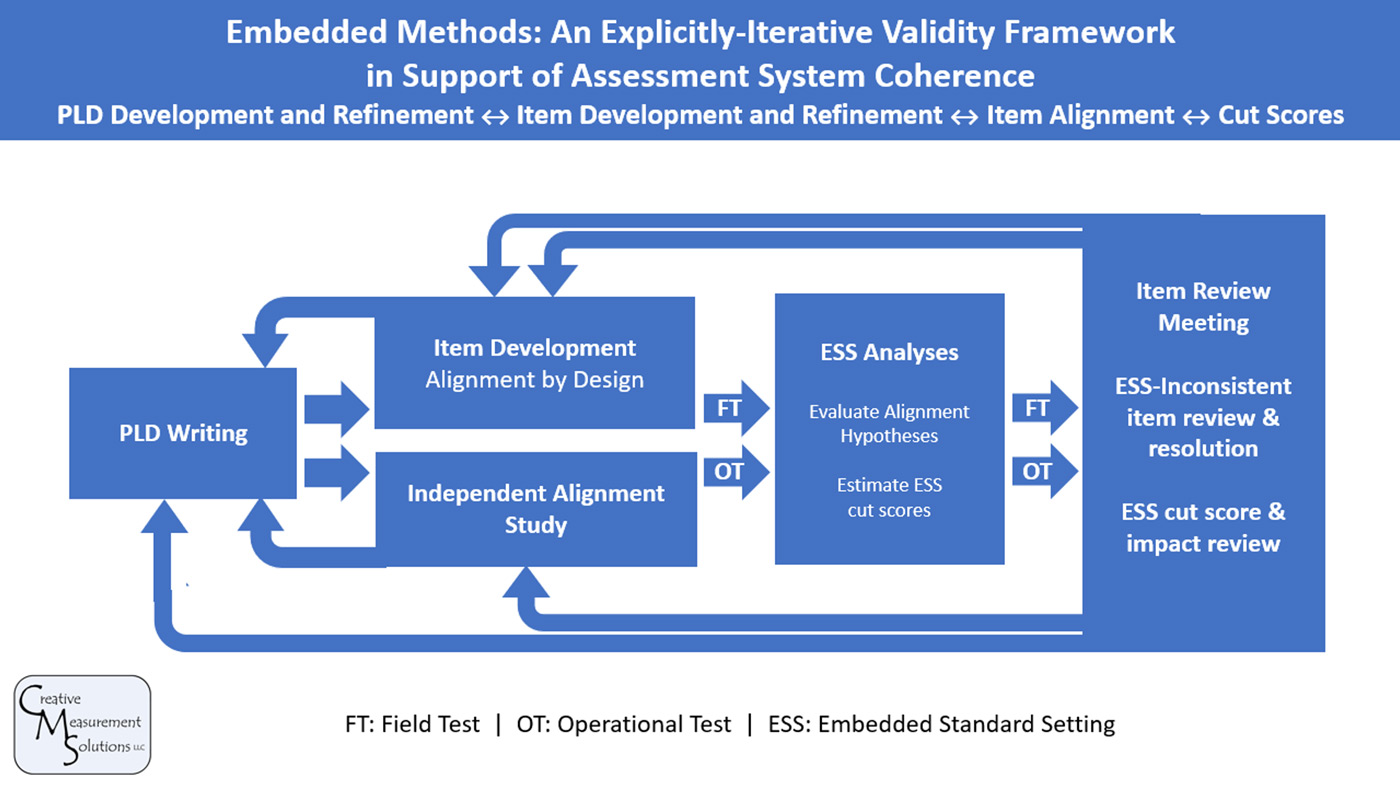
ESS was originally conceived as a practical approach to standard setting under a PAD framework. However, supporting the requirements of ESS adds value to an assessment system that extends well beyond the estimation of cut scores—it supports assessment system coherence. Embedded Methods refers to the integrated and iterative set of processes and procedures that span the assessment lifecycle under ESS and support the coherence of, and add value to, various assessment system components as shown in the Embedded Methods Validity Framework.

What do we mean by assessment system coherence? Assessment system coherence is manifest when the various assessment components form an internally consistent system. For example:

a. PLDs should clearly and comprehensively articulate the claims and measurement targets associated with the assessment of interest,

b. items should provide evidence for the claims and measurement targets attributed to students in specified performance levels,

c. items should be aligned to performance levels, preferably by design, but also an outcome of an independent alignment study,

d. empirical data should support SME’s hypothesized Item-PLD alignments, and

e. cut scores should have empirical data supporting the evidentiary relationship between assessment items and claims; that is, examinees in each performance level should have a strong likelihood of success on the items aligned to the claims and measurement targets of the specified achievement levels.

Assessment system coherence is supported by the application of principled assessment design. However, the application of PAD does not guarantee coherence; rather, coherence results from adherence to the Embedded Methods Validity Framework. Additional details about the Embedded Methods Validity Framework are available in Lewis & Forte (2021).

ESS (Lewis & Cook, 2020) and Embedded Methods (Lewis & Forte, 2021) will be used for the SIPS project to (a) support the development of well-articulated PLDs, (b) support test design and development, (c) directly measure the knowledge and skills that students demonstrate on each task, (d) estimate cut scores used to place students in performance levels, and (e) potentially monitor and measure longitudinal growth over the school year.